Solution 35314: Finding Critical Points Using the TI-Nspire™ CAS Family.
How can critical points be found using the TI-Nspire CAS family?
The critical points of a function are the points where the derivative is equal to zero, reach a local minimum, or reach a local maximum. The following illustrates how to use the differentiate and solve functions to find critical points.
Example: Find the critical points using the solver and differentiation commands on the home screen for the following function:
f(x)= x^3+x^2-5x-5
The first step to finding the critical points is to differentiate the above function:
1) Press [home] and choose to add a Calculator.
2) Press [menu] [4] [1].
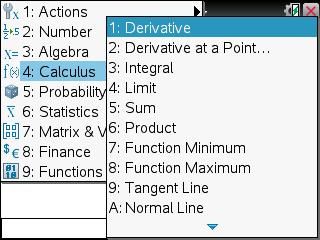
3) Press [X] [tab].
4) Press [X] [^] [3] [tab].
5) Press [+] [X] [x2] [-] [5] [X] [-] [5] [,] [X] [)].
6) Press [enter].
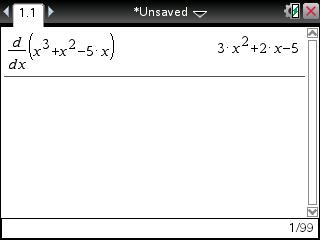
To find one of the critical points the user will need to set the derivative (shown above) equal to zero and solve for x:
1) Press [menu] [3] [1].
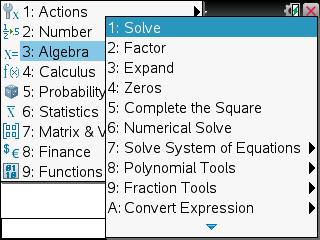
2) Press [3] [X] [x2] [+] [2] [X] [-] [5].
3) Press [=] [0] [,] [X] [)].
4) Press [enter].

Since there are two answers for the following function, there will be two sets of critical points on this function.
Now to solve for the additional points, plug x into the original equation:
1) Press [X] [^] [3] [tab].
2) Press [+] [X] [x2].
3) Press [-] [5] [X] [-] [5].
4) Press [ctrl] [=] and choose "|".
5) Press [X] [=] [1].
6) Press [enter].
7) Press [X] [^] [3] [tab].
8) Press [+] [X] [x2].
9) Press [-] [5] [X] [-] [5].
10) Press [ctrl] [=] and choose "|".
11) Press [X] [=] [ctrl] [÷].
12) Press [(-)] [5] [tab] [3].
13) Press [enter].

The answers show the y coordinates for the two critical points on this function. So the critical values for the function f(x)= x^3+x^2-5x-5 are (-5/3,40/27) and (1,-8).
Please see the TI-Nspire CX CAS and TI-Nspire CAS guidebooks for additional information.
